The Schröder-Bernstein theorem is one of most fundamental facts in set theory. Here we give an easy-to-follow proof of it.
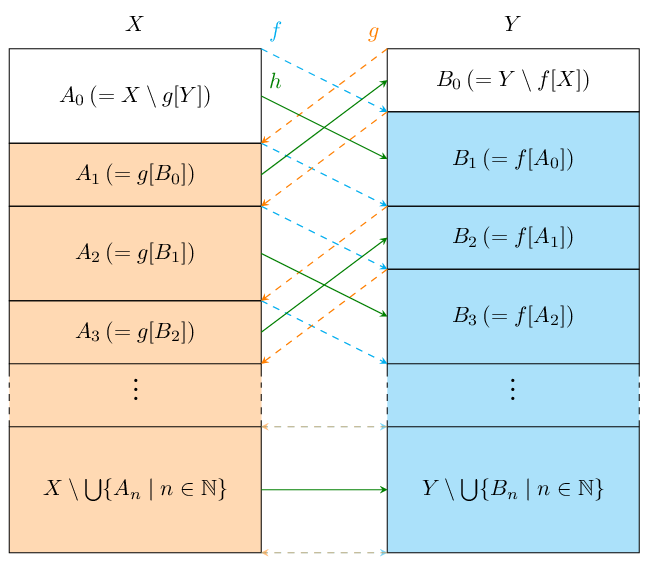
Let \(f: X \rightarrow Y\) and \(g: Y \rightarrow X\) be injective. To find a bijection \(h: X \rightarrow Y\), first we define a couple of sequences of sets, \(\{A_n \subset X \mid n \in \mathbb{N}\}\) and \(\{B_n \subset Y \mid n \in \mathbb{N}\},\) as follows:
\[A_0 := X \setminus g[Y] = \{x \in X \mid \not \exists y \in Y (x = g(y))\};\]\[B_0 := Y \setminus f[X] = \{y \in Y \mid \not \exists x \in X (f(x) = y)\};\]\[A_{n+1} := g[B_n];\]\[B_{n+1} := f[A_n].\]
Note that \(A_n\) are pairwise disjoint for different \(n\)s and \(B_n\) are too, which are provable by simultaneous induction on \(n\), because \(f\) and \(g\) are injective.
Define \(h: X \rightarrow Y\) by:
\[h(x) := \begin{cases}g^{-1}(x) & \text{if}\ x \in A_{2n+1} \text{for some}\ n\\f(x) & \text{otherwise}\end{cases}\]
which is well-defined since the restriction of \(g\) to \(B_{2n}\) is onto \(A_{2n+1}\).
The following figure illustrates the above definitions:

Our proof is done by remarking that \(f[X \setminus \bigcup \{A_n \mid n \in \mathbb{N}\}] = Y \setminus \bigcup \{B_n \mid n \in \mathbb{N}\}\) (and, of course symmmetrically \(g[Y \setminus \bigcup \{B_n \mid n \in \mathbb{N}\}] = X \setminus \bigcup \{A_n \mid n \in \mathbb{N}\},\) too).
It is now straightforward to see why the resulting bijection is not computable in general even with the original pair of injections as oracles; given \(x \in X\), you cannot decide whether \(x\) belongs to \(A_{2n+1}\) for some \(n\) or not in finitely many steps. Yet the above proof does not employ the axiom of choice.
One more thing to note is that fixed points of \(g \circ f\) are, if any, always outside of \(A_n\)s. More generally, any periodic point of \(g \circ f\) resides outside of \(A_n\)s.